Cross Section for Many Lines using MODIT

Update: September 3/2021, Hajime Kawahara

We demonstarte the Modified Discrete Integral Transform (MODIT), which is the modified version of DIT for exojax. MODIT uses the evenly-spaced logarithm grid (ESLOG) as a wavenumber dimension. MODIT takes advantage especially for the case that the number of the molecular line is large (typically > 1000). We here compare the results by MODIT with the direct computation (LPF).

import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
import jax.numpy as jnp
plt.style.use('bmh')

from exojax.spec.hitran import SijT, doppler_sigma, gamma_hitran, gamma_natural
from exojax.spec import moldb

# Setting wavenumber bins and loading HITRAN database
nus=np.logspace(np.log10(1900.0),np.log10(2300.0),350000,dtype=np.float64)
R=(len(nus)-1)/np.log(nus[-1]/nus[0]) #resolution

mdbCO=moldb.MdbHit('05_hit12.par',nus)
# set T, P and partition function
Mmol=28.01 # molecular weight
Tfix=1000.0 # we assume T=1000K
Pfix=1.e-3 # we compute P=1.e-3 bar
Ppart=Pfix #partial pressure of CO. here we assume a 100% CO atmosphere.
qt=mdbCO.Qr_layer_HAPI([Tfix])[0]

# compute Sij, gamma_L, sigmaD
Sij=SijT(Tfix,mdbCO.logsij0,mdbCO.nu_lines,mdbCO.elower,qt)
gammaL = gamma_hitran(Pfix,Tfix, Ppart, mdbCO.n_air, \
                      mdbCO.gamma_air, mdbCO.gamma_self) \
+ gamma_natural(mdbCO.A)

MODIT uses the normalized quantities by \(d \nu_\mathrm{line} \equiv \nu/R\), where R is the spectral resolution. In this case, the normalized Doppler width (nsigmaD) is common for the same isotope, \(\sqrt{\frac{k_B T}{m_u M}}*R\), where \(M\) is molecular mass \(m_u\) is the atomic mass unit. This can be computed using hitran.normalized_doppler_sigma. Then, we use a 2D DIT grid with the dimensions of the normalized gammaL and ESLOG grid \(q = R \log{\nu}\).

from exojax.spec.hitran import normalized_doppler_sigma
dv_lines=mdbCO.nu_lines/R
nsigmaD=normalized_doppler_sigma(Tfix,Mmol,R)
ngammaL=gammaL/dv_lines

MODIT uses a grid of ngammaL, and wavenumber. ditgrid makes a 1D grid for ngamma.

from exojax.spec.modit import ditgrid
ngammaL_grid=ditgrid(ngammaL)

# we can change the resolution using res option
#ngammaL_grid=ditgrid(ngammaL,res=0.1)

#show the grids
plt.plot(mdbCO.nu_lines,ngammaL,".")
for i in ngammaL_grid:
    plt.axhline(i,lw=1,alpha=0.5,color="C1")
plt.xlabel("wavenumber")
plt.ylabel("normalized gammaL")

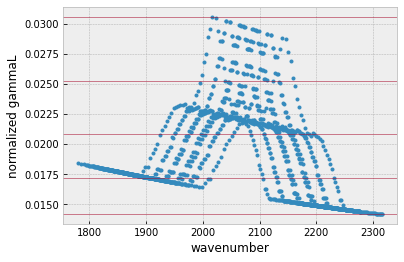
We need to precompute the contribution for wavenumber and pmarray. These can be computed using init_modit:

from exojax.spec import initspec
cnu,indexnu,R,pmarray=initspec.init_modit(mdbCO.nu_lines,nus)

Let’s compute the cross sectio using modit.xsvector.

from exojax.spec.modit import xsvector
xs=xsvector(cnu,indexnu,R,pmarray,nsigmaD,ngammaL,Sij,nus,ngammaL_grid)

Also, we here try the direct computation using LPF for the comparison purpose

from exojax.spec import xsection
sigmaD=doppler_sigma(mdbCO.nu_lines,Tfix,Mmol)
xsv=xsection(nus,mdbCO.nu_lines,sigmaD,gammaL,Sij,memory_size=30)

100%|███████████████████████████████████████████| 63/63 [00:02<00:00, 27.13it/s]

fig=plt.figure(figsize=(10,5))
ax=fig.add_subplot(211)
plt.plot(nus,xs,lw=1,alpha=0.5,label="MODIT")
plt.plot(nus,xsv,lw=1,alpha=0.5,label="Direct LPF")
plt.legend(loc="upper right")
plt.ylabel("Cross Section (cm2)")
ax=fig.add_subplot(212)
plt.plot(nus,xsv-xs,lw=2,alpha=0.5,label="MODIT")
plt.ylabel("LPF - DIT (cm2)")
plt.legend(loc="upper left")
plt.show()

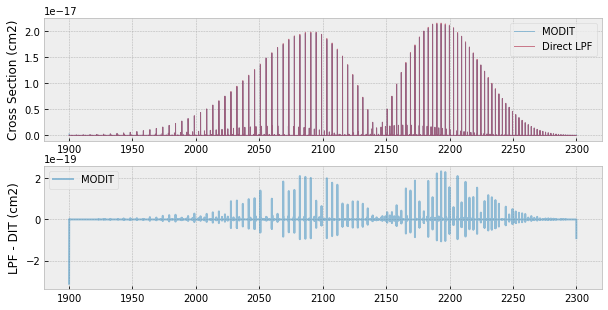
There is about 1 % deviation between LPF and MODIT.

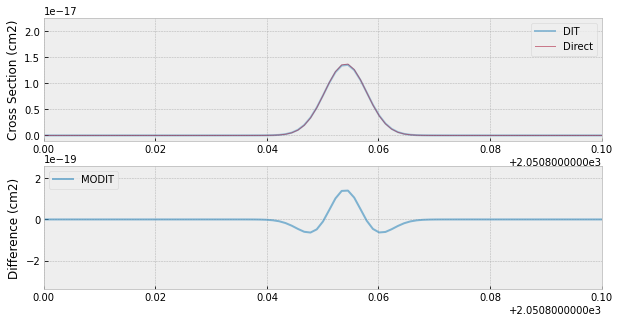
fig=plt.figure(figsize=(10,5))
ax=fig.add_subplot(211)
plt.plot(nus,xs,lw=2,alpha=0.5,label="DIT")
plt.plot(nus,xsv,lw=1,alpha=0.5,label="Direct")
plt.legend(loc="upper right")
plt.xlim(2050.8,2050.9)
plt.ylabel("Cross Section (cm2)")
ax=fig.add_subplot(212)
plt.plot(nus,xsv-xs,lw=2,alpha=0.6,label="MODIT")
plt.legend(loc="upper left")
plt.ylabel("Difference (cm2)")
plt.xlim(2050.8,2050.9)
plt.savefig("fine_grid.png")