🐶 Bayes Inference of a Real Spectrum of Luhman 16A (MODIT)

Update: Nov 10/2021, Hajime Kawahara

In this tutorial, we provide a tutorial for the MOTIT (a rapid opacity calculator) version of the HMC-NUTS fitting using NumPyro to the high-dispersion spectrum of Luhman 16A (Crossfield+2014). This is same as Case II (w/ GP) in 🐱 Bayes Inference of a Real Spectrum of Luhman 16A (Direct LPF) except for the opacity calculator. As the goal of this tutorial, we want to fit the exojax model to the high-dispersion data as

See the directories of examples/LUH16A/FidEMbug_modit for the full code. First, we import basic modules and some modules from jax,

# basic modules
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

# JAX
import jax.numpy as jnp
from jax import random
from jax import vmap, jit

and, many modules and functions from ExoJAX.

# ExoJAX
from exojax.spec import planck, moldb, contdb, response, molinfo, dit, modit, initspec
from exojax.spec.exomol import gamma_exomol
from exojax.spec.hitran import SijT, doppler_sigma, gamma_natural, gamma_hitran
from exojax.spec.hitrancia import read_cia, logacia
from exojax.spec.rtransfer import rtrun, dtauM, dtauCIA, nugrid, pressure_layer
from exojax.spec.evalline import mask_weakline
from exojax.spec.limb_darkening import ld_kipping
from exojax.spec.modit import exomol,xsmatrix,setdgm_exomol, minmax_dgmatrix

from exojax.utils.afunc import getjov_gravity
from exojax.utils.instfunc import R2STD
from exojax.utils.constants import RJ, pc
from exojax.utils.gpkernel import gpkernel_RBF

To fit the model to real high-resolution spectra, we usually need some information on absolute flux. Here, we just use the value from the mid-resolution spectrum.

# FLUX reference
Fabs_REF2=2.7e-12 #absolute flux (i.e. flux@10pc) erg/s/cm2/um Burgasser+ 1303.7283 @2.29um
fac0=RJ**2/((10.0*pc)**2)  #nomralize by RJ
Fref=(2.29**2)*Fabs_REF2/fac0/1.e4 #erg/cm2/s/cm-1 @ 2.3um

Loading the real data of Luhman-16A by Crossfield+2014.

# Loading spectrum
dat=pd.read_csv("../data/luhman16a_spectra_detector1.csv",delimiter=",")
wavd=(dat["wavelength_micron"].values)*1.e4 #AA
nusd=1.e8/wavd[::-1]
fobs=(dat["normalized_flux"].values)[::-1]
err=(dat["err_normalized_flux"].values)[::-1]

Here we define the atmospheric layer (100 layers) and some qunatities for the atmospheric model.

# ATMOSPHERIC LAYER
Pref=1.0 # Reference pressure for a T-P model (bar)
NP=100
Parr, dParr, k=pressure_layer(NP=NP)
mmw=2.33 # Mean molecular weight
ONEARR=np.ones_like(Parr) # ones_array for MMR
molmassCO=molinfo.molmass("CO") # molecular mass (CO)
molmassH2O=molinfo.molmass("H2O") # molecular mass (H2O)

Assuming the instrumental resolution… Yes, beta is the standard deviation of the Gaussian.

# Instrument
beta=R2STD(100000.) #std of gaussian from R=100000.

# LOADING CIA
mmrH2=0.74 # mean molecualr weight of H2 for CIA
mmrHe=0.25 # mean molecualr weight of He for CIA
molmassH2=molinfo.molmass("H2")
molmassHe=molinfo.molmass("He")
vmrH2=(mmrH2*mmw/molmassH2)
vmrHe=(mmrHe*mmw/molmassHe)

Here, we set the wavenumber grid, with the target range between ws and we AA, but having a margin +- 5 AA.

# Loading Molecular datanase and  Reducing Molecular Lines
Nx=4500    # number of wavenumber bins (nugrid) for fit
ws=22876.0 # AA
we=23010.0 # AA
nus,wav,res=nugrid(ws-5.0,we+5.0,Nx,unit="AA",xsmode="modit") # set nugrid

Some masking.

# Masking data
mask=(ws<wavd[::-1])*(wavd[::-1]<we) # data fitting range
mask=mask*((22898.5>wavd[::-1])+(wavd[::-1]>22899.5))  # Additional mask to remove a strong telluric
fobsx=fobs[mask]
nusdx=nusd[mask]
wavdx=1.e8/nusdx[::-1]
errx=err[mask]

Loading exomol databases for CO and H2O…

# Loading molecular database
mdbCO=moldb.MdbExomol('.database/CO/12C-16O/Li2015',nus)
mdbH2O=moldb.MdbExomol('.database/H2O/1H2-16O/POKAZATEL',nus,crit=1.e-46)

and CIA from HITRAN.

# LOADING CIA
cdbH2H2=contdb.CdbCIA('.database/H2-H2_2011.cia',nus)
cdbH2He=contdb.CdbCIA('.database/H2-He_2011.cia',nus)

This example uses Modified Discrete Integral Transform (MODIT). We do not need to reduce the number of lines. See Benchmark: LPF vs MODIT. Here is the initialization of MODIT.

# MODIT settings
cnu_CO, indexnu_CO, R_CO, pmarray_CO=initspec.init_modit(mdbCO.nu_lines,nus)
cnu_H2O, indexnu_H2O, R_H2O, pmarray_H2O=initspec.init_modit(mdbH2O.nu_lines,nus)

# Precomputing gdm_ngammaL
res=0.2 # MODIT grid resolution
fT = lambda T0,alpha: T0[:,None]*(Parr[None,:]/Pref)**alpha[:,None]
T0_test=np.array([1000.0,1700.0,1000.0,1700.0])
alpha_test=np.array([0.15,0.15,0.05,0.05])
dgm_ngammaL_CO=setdgm_exomol(mdbCO,fT,Parr,R_CO,molmassCO,res,T0_test,alpha_test)
dgm_ngammaL_H2O=setdgm_exomol(mdbH2O,fT,Parr,R_H2O,molmassH2O,res,T0_test,alpha_test)

We are now ready for an HMC-NUTS fitting!

# HMC-NUTS FITTING PART
from numpyro import sample
import numpyro.distributions as dist
from numpyro.infer import MCMC, NUTS
from numpyro.infer import Predictive
from numpyro.diagnostics import hpdi

# Some constants for fitting
baseline=1.07 #(baseline for a CIA photosphere in the observed (normaized) spectrum)
maxMMR_CO=0.01
maxMMR_H2O=0.005

Define the model.

# Model
def model_c(nu1,y1,e1):
    Rp = sample('Rp', dist.Uniform(0.5,1.5))
    Mp = sample('Mp', dist.Normal(33.5,0.3))
    RV = sample('RV', dist.Uniform(26.0,30.0))
    MMR_CO = sample('MMR_CO', dist.Uniform(0.0,maxMMR_CO))
    MMR_H2O = sample('MMR_H2O', dist.Uniform(0.0,maxMMR_H2O))
    T0 = sample('T0', dist.Uniform(1000.0,1700.0))
    alpha = sample('alpha', dist.Uniform(0.05,0.15))
    vsini = sample('vsini', dist.Uniform(10.0,20.0))

    # Kipping Limb Darkening Prior
    q1 = sample('q1', dist.Uniform(0.0,1.0))
    q2 = sample('q2', dist.Uniform(0.0,1.0))
    u1,u2=ld_kipping(q1,q2)

Set the GP hyperparameters

#def model_c(nu1,y1,e1): (continued)
   # GP
   logtau = sample('logtau', dist.Uniform(-1.5,0.5)) #tau=1 <=> 5A
   tau=10**(logtau)
   loga = sample('loga', dist.Uniform(-4.0,-2.0))
   a=10**(loga)

   #gravity
   g=getjov_gravity(Rp,Mp)

   # T-P model
   Tarr = T0*(Parr/Pref)**alpha

   # Line computation
   qt_CO=vmap(mdbCO.qr_interp)(Tarr)
   qt_H2O=vmap(mdbH2O.qr_interp)(Tarr)

spec.modit.exomol is a convenient way to obtain the quantities for line profile.

#def model_c(nu1,y1,e1): (continued)
  def obyo(y,tag,nusdx,nus,mdbCO,mdbH2O,cdbH2H2,cdbH2He):
      #CO
      SijM_CO,ngammaLM_CO,nsigmaDl_CO=exomol(mdbCO,Tarr,Parr,R_CO,molmassCO)
      xsm_CO=xsmatrix(cnu_CO,indexnu_CO,R_CO,pmarray_CO,nsigmaDl_CO,ngammaLM_CO,SijM_CO,nus,dgm_ngammaL_CO)
      dtaumCO=dtauM(dParr,jnp.abs(xsm_CO),MMR_CO*ONEARR,molmassCO,g)

      #H2O
      SijM_H2O,ngammaLM_H2O,nsigmaDl_H2O=exomol(mdbH2O,Tarr,Parr,R_H2O,molmassH2O)
      xsm_H2O=xsmatrix(cnu_H2O,indexnu_H2O,R_H2O,pmarray_H2O,nsigmaDl_H2O,ngammaLM_H2O,SijM_H2O,nus,dgm_ngammaL_H2O)
      dtaumH2O=dtauM(dParr,jnp.abs(xsm_H2O),MMR_H2O*ONEARR,molmassH2O,g)

      #CIA
      dtaucH2H2=dtauCIA(nus,Tarr,Parr,dParr,vmrH2,vmrH2,\
                        mmw,g,cdbH2H2.nucia,cdbH2H2.tcia,cdbH2H2.logac)
      dtaucH2He=dtauCIA(nus,Tarr,Parr,dParr,vmrH2,vmrHe,\
                        mmw,g,cdbH2He.nucia,cdbH2He.tcia,cdbH2He.logac)

      dtau=dtaumCO+dtaumH2O+dtaucH2H2+dtaucH2He
      sourcef = planck.piBarr(Tarr,nus)

      Ftoa=Fref/Rp**2
      F0=rtrun(dtau,sourcef)/baseline/Ftoa

      Frot=response.rigidrot(nus,F0,vsini,u1,u2)
      mu=response.ipgauss_sampling(nusdx,nus,Frot,beta,RV)
      cov = gpkernel_RBF(nu1,tau,a,e1)

Here, in the case of a GP modeling of the noise, just define the GP kernel and use dist.MultivariateNormal.

#def model_c(nu1,y1,e1): (continued)
      sample(tag, dist.MultivariateNormal(loc=mu, covariance_matrix=cov), obs=y)

  obyo(y1,"y1",nu1,nus,mdbCO,mdbH2O,cdbH2H2,cdbH2He)

Then, run the HMC-NUTS. Note that we here use forward mode (forward differentiation) by ‘forward_mode_differentiation=True’ in NUTS. Since ExoJAX v1.1, we can also use the reverse mode ‘forward_mode_differentiation=False’ in NUTS.

# Run a HMC-NUTS
rng_key = random.PRNGKey(0)
rng_key, rng_key_ = random.split(rng_key)
num_warmup, num_samples = 500, 1000
kernel = NUTS(model_c,forward_mode_differentiation=True)
mcmc = MCMC(kernel, num_warmup=num_warmup, num_samples=num_samples)
mcmc.run(rng_key_, nu1=nusdx, y1=fobsx, e1=errx)
print("End HMC")

That’s all! The rest part is just for saving and plotting.

# Post-processing
posterior_sample = mcmc.get_samples()
np.savez("npz/savepos.npz",[posterior_sample])

pred = Predictive(model_c,posterior_sample,return_sites=["y1"])
nu = nus
predictions = pred(rng_key_,nu1=nu,y1=None,e1=errx)
median_mu = jnp.median(predictions["y1"],axis=0)
hpdi_mu = hpdi(predictions["y1"], 0.9)
np.savez("npz/saveplotpred.npz",[wavdx,fobsx,errx,median_mu,hpdi_mu])

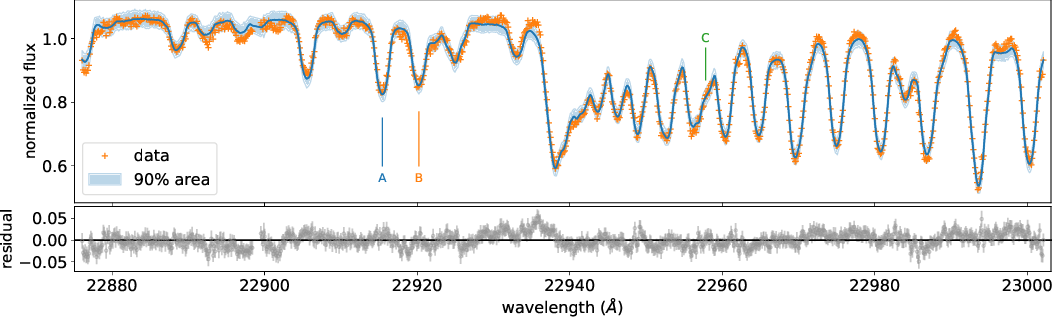
fig, ax = plt.subplots(nrows=1, ncols=1, figsize=(20,6.0))
ax.plot(wavdx[::-1],median_mu,color="C0")
ax.plot(wavdx[::-1],fobsx,"+",color="C1",label="data")

# Annotation for some lines
red=(1.0+28.07/300000.0) #for annotation
ax.plot([22913.3*red,22913.3*red],[0.6,0.75],color="C0",lw=1)
ax.plot([22918.07*red,22918.07*red],[0.6,0.77],color="C1",lw=1)
ax.plot([22955.67*red,22955.67*red],[0.6,0.68],color="C2",lw=1)
plt.text(22913.3*red,0.55,"A",color="C0",fontsize=12,horizontalalignment="center")
plt.text(22918.07*red,0.55,"B",color="C1",fontsize=12,horizontalalignment="center")
plt.text(22955.67*red,0.55,"C",color="C2",fontsize=12,horizontalalignment="center")
ax.fill_between(wavdx[::-1], hpdi_mu[0], hpdi_mu[1], alpha=0.3, interpolate=True,color="C0",
                label="90% area")
plt.xlabel("wavelength ($\AA$)",fontsize=16)
plt.legend(fontsize=16)
plt.tick_params(labelsize=16)
plt.savefig("npz/results.pdf", bbox_inches="tight", pad_inches=0.0)
plt.savefig("npz/results.png", bbox_inches="tight", pad_inches=0.0)

Arviz is very useful for plotting, such as the corner plot, the trace plot and so on.

# ARVIZ part
import arviz
rc = {
"plot.max_subplots": 1024,
}

try:
    arviz.rcParams.update(rc)
    arviz.plot_pair(arviz.from_numpyro(mcmc),kind='kde',divergences=False,marginals=True)
    plt.savefig("npz/cornerall.png")
    except:
    print("failed corner")

try:
    pararr=["Mp","Rp","T0","alpha","MMR_CO","MMR_H2O","vsini","RV","q1","q2","logtau","loga"]
    arviz.plot_trace(mcmc, var_names=pararr)
    plt.savefig("npz/trace.png")
except:
    print("failed trace")