Quatum states of Carbon Monoxide and Fortrat Diagram

We here see the quantum states of Carbon Monoxide. Also, to see how the band head appears, we would like to plot the Fortrat diagram with a given quantum number and interval. To do so, we use optional_quantum_states=True option in api.MdbExomol.

from exojax.spec import api
emf='CO/12C-16O/Li2015'
mdb = api.MdbExomol(emf, None, optional_quantum_states=True)

/home/kawahara/exojax/src/exojax/utils/molname.py:133: FutureWarning: e2s will be replaced to exact_molname_exomol_to_simple_molname.
  warnings.warn(
/home/kawahara/exojax/src/exojax/spec/api.py:153: UserWarning: nurange=None. Nonactive mode.
  warnings.warn("nurange=None. Nonactive mode.", UserWarning)

HITRAN exact name= (12C)(16O)
Background atmosphere:  H2
Reading CO/12C-16O/Li2015/12C-16O__Li2015.trans.bz2
DataFrame (self.df) available.

Check DataFrame. We see Li2015 contains the vibrational states for lower and upper states, v_l, v_u.

mdb.df[0:2]
# i_upper i_lower A nu_lines gup jlower jupper elower v_l v_ukp_l kp_u Sij0
0 84 421.155e-06 2.40559 3 0 1 66960.7 41 41e e 3.81197e-164
1 83 411.161e-06 2.44177 3 0 1 65819.9 40 40e e 9.66303e-162

The Rovib transition changes both rotational and vibrational quantum states. We here investigate the vibrational quantum state \(\nu\). Let’s check how many \(\Delta \nu\) Li2015 database contains:

import numpy as np
dv = mdb.df["v_u"]-mdb.df["v_l"]
np.unique(dv.values)

array([ 0,  1,  2,  3,  4,  5,  6,  7,  8,  9, 10, 11])

So, we have 12 different \(\Delta \nu\). Let’s plot them.

import matplotlib.pyplot as plt

fig = plt.figure(figsize=(15, 4))
ax = fig.add_subplot(111)
for i, udv in enumerate(np.unique(dv.values)):
    mask = dv == udv
    mdf = mdb.df[mask]
    ax.plot(mdf["nu_lines"].values,
             mdf["Sij0"].values,
             ".",
             alpha=0.3,
             #alpha=0.01 + 0.005 * i,
             color="gray")
    ax.text(
        np.sum(mdf["nu_lines"].values * mdf["Sij0"].values) /
        np.sum(mdf["Sij0"].values), 1.e2*np.max(mdf["Sij0"].values),"$\\Delta \\nu=$"+str(udv))

for mic in [0.5,1,2,3,4,5,10,20]:
    x = 1.e4/mic
    plt.axvline(x,alpha=0.2,color="gray")
    #plt.text(x,1.e-210,str(mic)+" $\\mu$m",rotation="90")
    plt.text(x,1.e-39,str(mic)+" $\\mu$m",rotation="90")
plt.yscale("log")
plt.ylim(1.e-41,1.e-13)
plt.tick_params(labelsize=14)
plt.xlabel("wavenumber (cm-1)",fontsize=14)
plt.ylabel("line strength",fontsize=14)
plt.savefig("co_dnu.png", bbox_inches="tight", pad_inches=0.1)
plt.show()
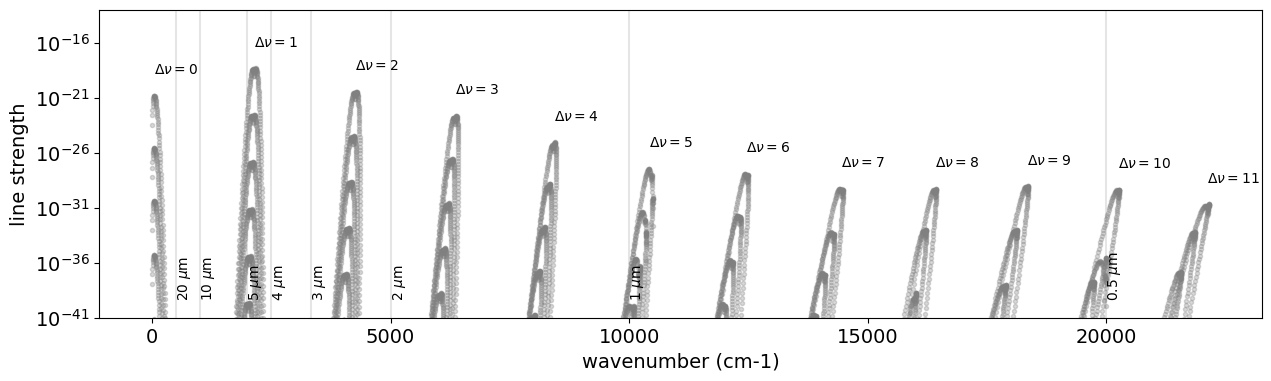
../_images/Fortrat_8_0.png

Let’s go deeper! Expand this for \(\Delta \nu=2\) (K-band feature).

dv = mdb.df["v_u"] - mdb.df["v_l"]
dJ = mdb.df["jupper"] - mdb.df["jlower"]

fig = plt.figure(figsize=(10, 5))
for i, vl in enumerate(np.unique(mdb.df["v_l"].values)):
    mask = (dv == 2) * (dJ == 1) * (mdb.df["v_l"] == vl)
    vdf = mdb.df[mask]
    plt.plot(vdf["nu_lines"].values, vdf["Sij0"].values, ".", color="black")
    if i < 10:
        plt.text(np.nanmean(vdf["nu_lines"].values),
                 8 * np.nanmax(vdf["Sij0"].values),
                 "$\\nu_{lower}=$" + str(vl),
                 fontsize=12)
    mask = (dv == 2) * (dJ == -1) * (mdb.df["v_l"] == vl)
    vdf = mdb.df[mask]
    plt.plot(vdf["nu_lines"].values, vdf["Sij0"].values, ".", color="gray")

for mic in [2.3, 2.5, 2.7]:
    x = 1.e4 / mic
    plt.axvline(x, alpha=0.2, color="gray")
    #plt.text(x,1.e-210,str(mic)+" $\\mu$m",rotation="90")
    plt.text(x, 1.e-60, str(mic) + " $\\mu$m", rotation="90")

plt.text(3800.0,
         1.e-25,
         "$\\Delta J$ = -1, P-branch",
         color="gray",
         fontsize=14)
plt.text(4380.0,
         1.e-25,
         "$\\Delta J$ = 1, R-branch",
         color="black",
         fontsize=14)
plt.yscale("log")
plt.ylim(1.e-61, 1.e-13)
plt.xlim(3500, 4620)
plt.tick_params(labelsize=14)
plt.xlabel("wavenumber (cm-1)", fontsize=14)
plt.ylabel("line strength", fontsize=14)
plt.savefig("co_dnu_expand.png", bbox_inches="tight", pad_inches=0.1)
plt.show()
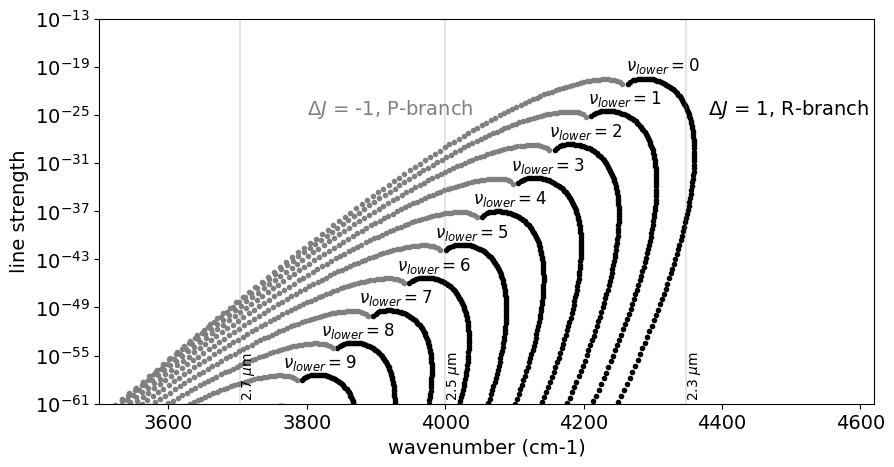
../_images/Fortrat_10_0.png

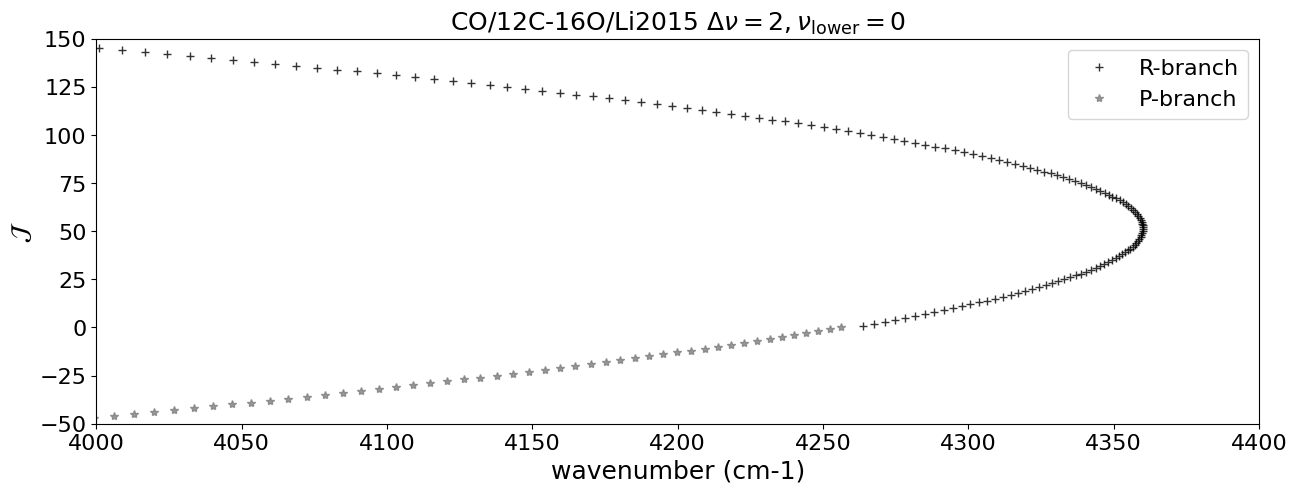
Using DataFrame, we pick up the lines with \(\Delta \nu = 2\), \(\Delta J = \pm 1\) (R, P-branch), and \(\nu = 0\) here.

dv = mdb.df["v_u"]-mdb.df["v_l"]
dJ = mdb.df["jupper"] - mdb.df["jlower"]
vmask = mdb.df["v_l"] == 0
mask_R = (dv == 2) * (dJ == 1) * vmask
mask_P = (dv == 2) * (dJ == -1) * vmask

df_R = mdb.df[mask_R]
df_P = mdb.df[mask_P]

Let’s plot the Fortrat diagram. The y-axis of the Fortart diagram is \(J_\mathrm{upper}\) for R-branch and \(- J_\mathrm{lower}\) for P-branch.

import matplotlib.pyplot as plt
fig = plt.figure(figsize=(15,5))
plt.plot(df_R["nu_lines"].values,df_R["jupper"].values,"+",alpha=0.8, color="black",label="R-branch")
plt.plot(df_P["nu_lines"].values,- df_P["jupper"].values,"*",alpha=0.8, color="gray",label="P-branch")
plt.tick_params(labelsize=16)
plt.xlabel("wavenumber (cm-1)", fontsize=18)
plt.ylabel("$\\mathcal{J}$", fontsize=18)
plt.legend(fontsize=16)
plt.title(emf+" $\\Delta \\nu = 2, \\nu_\\mathrm{lower} = 0$",fontsize=18)
plt.xlim(4000.,4400)
plt.ylim(-50,150)
plt.savefig("fortrat.png",  bbox_inches="tight", pad_inches=0.1)
plt.show()
../_images/Fortrat_14_0.png