Flux-based Emission with pure absorption

Uses ArtPureEmis class

The following is a typical example of code for calculating emission using fbased with the art class in ExoJAX. For pure absorption emission, ArtEmisPure is provided as the art class. To specify fbase, it is simply a matter of setting the option as rtsolver=”fbased2st” when calling it (although this is set by default).

from exojax.spec.atmrt import ArtEmisPure

art = ArtEmisPure(pressure_top=1.e-8,
                  pressure_btm=1.e2,
                  nlayer=100,
                  nu_grid=nu_grid,
                  rtsolver="fbased2st")

art.change_temperature_range(400.0, 1500.0) #sets temperature range
Tarr = art.powerlaw_temperature(1300.0, 0.1) # sets a powerlaw T-P profile
mmr_arr = art.constant_mmr_profile(0.1) # sets a constant mass mixing ratio
gravity = art.constant_gravity_profile(2478.57) #sets a constant gravity

# we here call OpaPremodit as opa just to compute xsmatrix
opa = OpaPremodit(mdb=mdb,
                  nu_grid=nu_grid,
                  diffmode=diffmode,
                  auto_trange=[art.Tlow, art.Thigh])
xsmatrix = opa.xsmatrix(Tarr, art.pressure)

dtau = art.opacity_profile_xs(xsmatrix, mmr_arr, opa.mdb.molmass, gravity) # computes optical depth profile
F0 = art.run(dtau, Tarr) # computes spectrum

Understands One-by-One

The upward flux of the n-th layer (with pressure of \(P_n\)) is connected to that of the (n-1)-th layer with transmission T and source function S.

\(F_{n} = \mathcal{T}_n F_{n+1} + (1-\mathcal{T}_n) \, \mathcal{S}_n\)

where \(P_{n-1} < P_n\). So, we need to specify a transmission and source function.

Source function

A black body emission as a source as,

\(\mathcal{S} = \pi B(T)\)

we can use piBarr.

>>> from exojax.spec import planck
    >>> sourcef = planck.piBarr(Tarr,nus)

Transmission for Pure Absorption: trans2E3

In this case, the transmission is given as

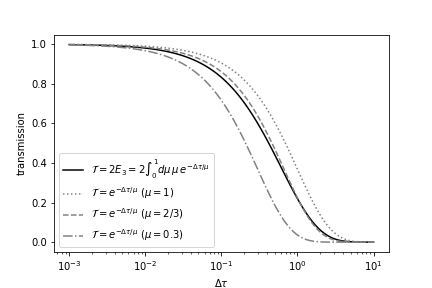
\(\mathcal{T}_n = 2 E_3(\Delta \tau_n ) = ( 1 - \Delta \tau_n) \exp{(- \Delta \tau_n)} + (\Delta \tau_n )^2 E_1(\Delta \tau_n )\)

where \(\Delta \tau_n\) is delta opacity in the n-th layer, \(E_j(x)\) is the exopential integral of the \(j\) -th order. In exojax, \(2 E_3(x)\) is available as

>>> from exojax.spec.rtransfer import trans2E3
>>> trans2E3(1.0)
DeviceArray(0.21938396, dtype=float32)

trans2E3 is auto-differentiable.

>>> from jax import grad
>>> grad(trans2E3)(1.0)
DeviceArray(-0.29698896, dtype=float32)

Here is \(\Delta \tau\) dependence of \(2 E_3(x)\):

trans2E3 is used in rtrun, which gives an emission spectral model with pure absorption. Then, rtrun has two inputs, one is the arrays of \(\Delta \tau_n\) and source funtion.

F0=rtrun(dtau,sourcef)

See “../tutorials/forward_modeling” to know how to use rtrun in a forward modeling. Note that exojax uses a linear algebraic formulation to solve the RT. The detail description is provided in Paper I .