The Voigt-Hjerting is defined as

$ H(x,a) = :raw-latex:`\frac{a}{\pi}` :raw-latex:`\int`_{-:raw-latex:`\infty`}^{:raw-latex:`\infty`} :raw-latex:`\frac{e^{-y^2}}{(x-y)^2 + a^2}` dy.$

In exojax, hjert is the Voigt-Hjerting function.

from exojax.spec import hjert
hjert(1.0,1.0)

Array(0.3047442, dtype=float32)

We can differentiate the Voigt-Hjerting function by \(x\). \(\partial_x H(x,a)\) is given by

from jax import grad
dhjert_dx=grad(hjert,argnums=0)
dhjert_dx(1.0,1.0)

Array(-0.19305044, dtype=float32, weak_type=True)

hjert is compatible to JAX. So, when you want to use array as input, you need to wrap it by jax.vmap.

import jax.numpy as jnp
from jax import vmap
import matplotlib.pyplot as plt

#input vector
x=jnp.linspace(-5,5,100)

#vectorized hjert H(x,a)
vhjert=vmap(hjert,(0,None),0)

#vectroized dH(x,a)/dx
vdhjert_dx=vmap(dhjert_dx,(0,None),0)

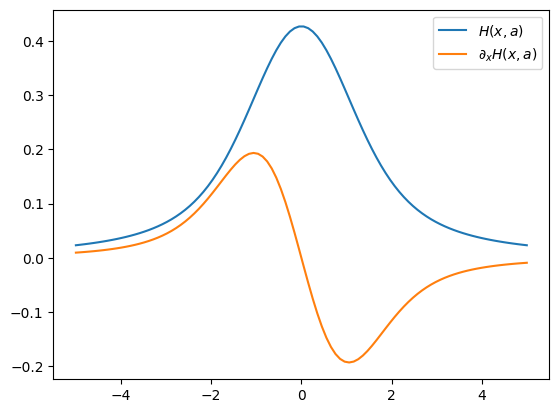
plt.plot(x, vhjert(x,1.0),label="$H(x,a)$")
plt.plot(x, vdhjert_dx(x,1.0),label="$\\partial_x H(x,a)$")
plt.legend()

<matplotlib.legend.Legend at 0x7f062c293820>