Optimization of a Voigt profile using JAXopt

from exojax.spec.lpf import voigt
import jax.numpy as jnp
import matplotlib.pyplot as plt
import jaxopt

Let’s optimize the Voigt function \(V(\nu, \beta, \gamma_L)\) using exojax! \(V(\nu, \beta, \gamma_L)\) is a convolution of a Gaussian with a STD of \(\beta\) and a Lorentian with a gamma parameter of \(\gamma_L\).

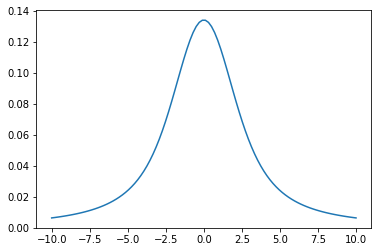
nu=jnp.linspace(-10,10,100)
plt.plot(nu, voigt(nu,1.0,2.0)) #beta=1.0, gamma_L=2.0

[<matplotlib.lines.Line2D at 0x7fbcef7569a0>]

optimization of a simple absorption model

Next, we try to fit a simple absorption model to mock data. The absorption model is

$ f= e^{-a V(:raw-latex:`\nu`,:raw-latex:beta,:raw-latex:gamma_L)}$

def absmodel(nu,a,beta,gamma_L):
    return jnp.exp(-a*voigt(nu,beta,gamma_L))

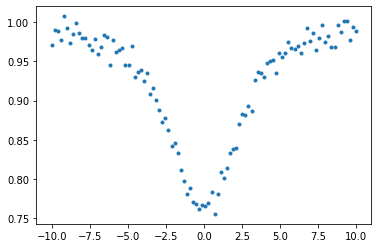
Adding a noise…

from numpy.random import normal
data=absmodel(nu,2.0,1.0,2.0)+normal(0.0,0.01,len(nu))
plt.plot(nu,data,".")

[<matplotlib.lines.Line2D at 0x7fb90d0398b0>]

Let’s optimize the multiple parameters

We define the objective function as \(obj = |d - f|^2\)

# loss or objective function
def objective(params):
    a,beta,gamma_L=params
    f=data-absmodel(nu,a,beta,gamma_L)
    g=jnp.dot(f,f)
    return g

# Gradient Descent

gd = jaxopt.GradientDescent(fun=objective, maxiter=10)
res = gd.run(init_params=(1.5,0.7,1.5))
params, state = res

params

(DeviceArray(1.9579332, dtype=float32, weak_type=True),
 DeviceArray(1.0382165, dtype=float32, weak_type=True),
 DeviceArray(1.8850585, dtype=float32, weak_type=True))

from numpy.random import normal
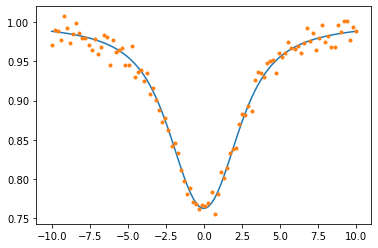
model=absmodel(nu,params[0],params[1],params[2])
plt.plot(nu,model)
plt.plot(nu,data,".")

[<matplotlib.lines.Line2D at 0x7fb90cf3d490>]

#NCG

gd = jaxopt.NonlinearCG(fun=objective, maxiter=100)
res = gd.run(init_params=(1.5,0.7,1.5))
params, state = res

params

(DeviceArray(1.9526778, dtype=float32),
 DeviceArray(1.0492882, dtype=float32),
 DeviceArray(1.8708111, dtype=float32))

from numpy.random import normal
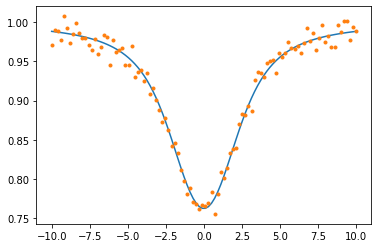
model=absmodel(nu,params[0],params[1],params[2])
plt.plot(nu,model)
plt.plot(nu,data,".")

[<matplotlib.lines.Line2D at 0x7fb90c0d6eb0>]